News

IncomeSCM: From tabular data set to time-series simulator and causal estimation benchmark

Sep 29, 2024

Evaluating observational estimators of causal effects demands information that is rarely available: unconfounded interventions and outcomes from the population of interest, created either by randomization or adjustment. As a result, it is customary to fall back on simulators when creating benchmark tasks. Simulators offer great control but are often too simplistic to make challenging tasks, either because they are hand-designed and lack the nuances of real-world data, or because they are fit to observational data without structural constraints. In this work, we propose a general, repeatable strategy for turning observational data into sequential structural causal models and challenging estimation tasks by following two simple principles: 1) fitting real-world data where possible, and 2) creating complexity by composing simple, hand-designed mechanisms. We implement these ideas in a highly configurable software package and apply it to the well-known Adult income data set to construct the \tt IncomeSCM simulator. From this, we devise multiple estimation tasks and sample data sets to compare established estimators of causal effects. The tasks present a suitable challenge, with effect estimates varying greatly in quality between methods, despite similar performance in the modeling of factual outcomes, highlighting the need for dedicated causal estimators and model selection criteria.

Active Preference Learning for Ordering Items In- and Out-of-Sample

Sep 29, 2024

Learning an ordering of items based on pairwise comparisons is useful when items are difficult to rate consistently on an absolute scale, for example, when annotators have to make subjective assessments. When exhaustive comparison is infeasible, actively sampling item pairs can reduce the number of annotations necessary for learning an accurate ordering. However, many algorithms ignore shared structure between items, limiting their sample efficiency and precluding generalization to new items. It is also common to disregard how noise in comparisons varies between item pairs, despite it being informative of item similarity. In this work, we study active preference learning for ordering items with contextual attributes, both in- and out-of-sample. We give an upper bound on the expected ordering error of a logistic preference model as a function of which items have been compared. Next, we propose an active learning strategy that samples items to minimize this bound by accounting for aleatoric and epistemic uncertainty in comparisons. We evaluate the resulting algorithm, and a variant aimed at reducing model misspecification, in multiple realistic ordering tasks with comparisons made by human annotators. Our results demonstrate superior sample efficiency and generalization compared to non-contextual ranking approaches and active preference learning baselines.

Pure Exploration in Bandits with Linear Constraints

Feb 4, 2024

We address the problem of identifying the optimal policy with a fixed confidence level in a multi-armed bandit setup, when \emph{the arms are subject to linear constraints}. Unlike the standard best-arm identification problem which is well studied, the optimal policy in this case may not be deterministic and could mix between several arms. This changes the geometry of the problem which we characterize via an information-theoretic lower bound. We introduce two asymptotically optimal algorithms for this setting, one based on the Track-and-Stop method and the other based on a game-theoretic approach. Both these algorithms try to track an optimal allocation based on the lower bound and computed by a weighted projection onto the boundary of a normal cone. Finally, we provide empirical results that validate our bounds and visualize how constraints change the hardness of the problem.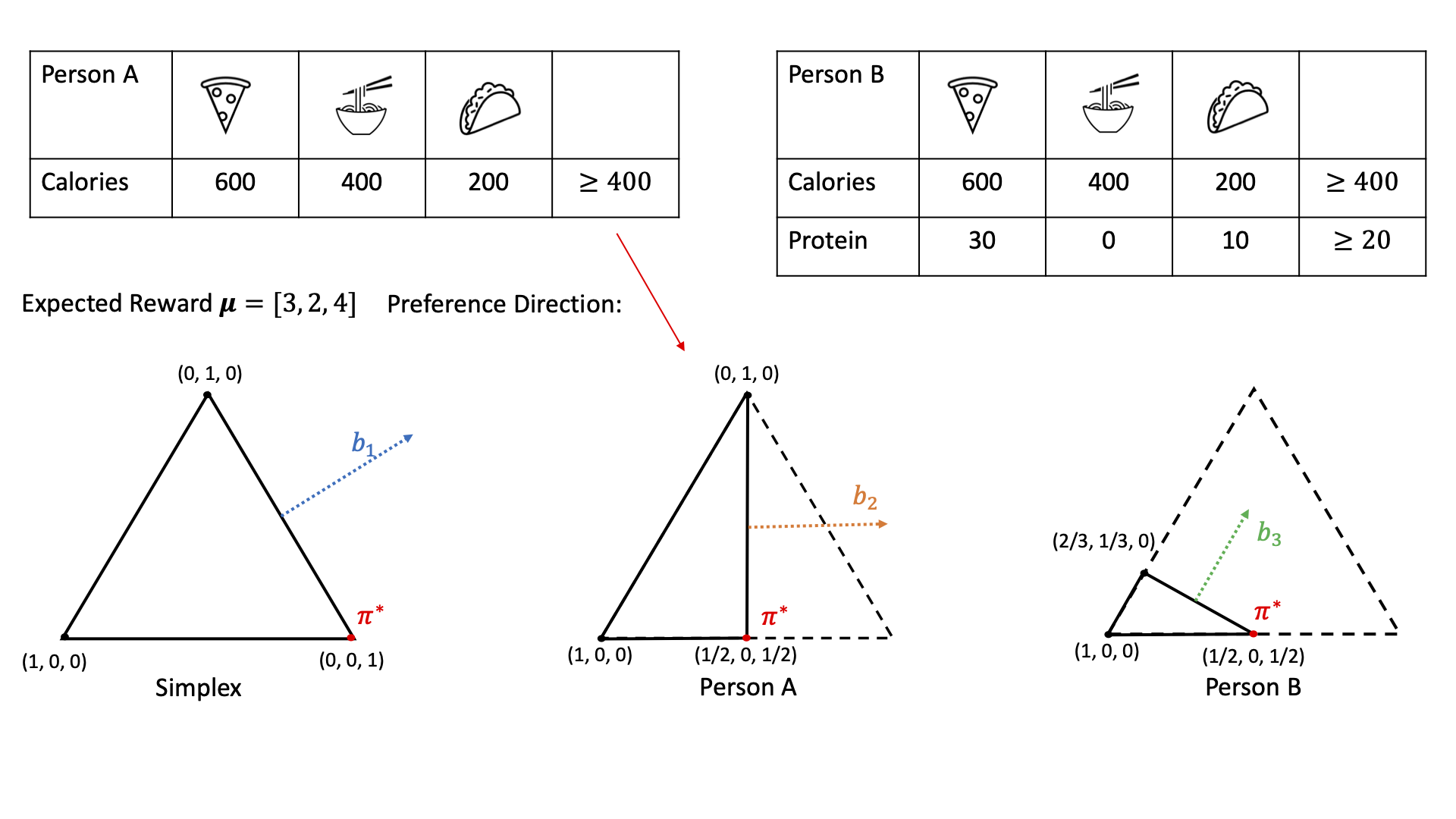

MINTY: Rule-based Models that Minimize the Need for Imputing Features with Missing Values

Oct 28, 2023

Rule models are often preferred in prediction tasks with tabular inputs as they can be easily interpreted using natural language and provide predictive performance on par with more complex models. However, most rule models’ predictions are undefined or ambiguous when some inputs are missing, forcing users to rely on statistical imputation models or heuristics like zero imputation, undermining the interpretability of the models. In this work, we propose fitting concise yet precise rule models that learn to avoid relying on features with missing values and, therefore, limit their reliance on imputation at test time. We develop MINTY, a method that learns rules in the form of disjunctions between variables that act as replacements for each other when one or more is missing. This results in a sparse linear rule model, regularized to have small dependence on features with missing values, that allows a trade-off between goodness of fit, interpretability, and robustness to missing values at test time. We demonstrate the value of MINTY in experiments using synthetic and real-world data sets and find its predictive performance comparable or favorable to baselines, with smaller reliance on features with missing values.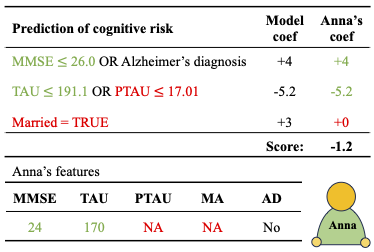

Patterns in the Sequential Treatment of Patients With Rheumatoid Arthritis Starting a Biologic or Targeted Synthetic Disease-Modifying Antirheumatic Drug: 10-Year Experience From a US-Based Registry

Oct 26, 2023

Developing and evaluating new treatment guidelines for rheumatoid arthritis (RA) based on observational data requires a quantitative understanding of patterns in current treatment practice with biologic and targeted synthetic disease-modifying antirheumatic drugs (b/tsDMARDs). We used data from the CorEvitas RA registry to study patients starting their first b/tsDMARD therapy, defined as the first line of therapy, between 2012 and the end of 2021. We identified treatment patterns as unique sequences of therapy changes following and including the first-line therapy. Therapy cycling was defined as switching back to a treatment from a previously used therapeutic class.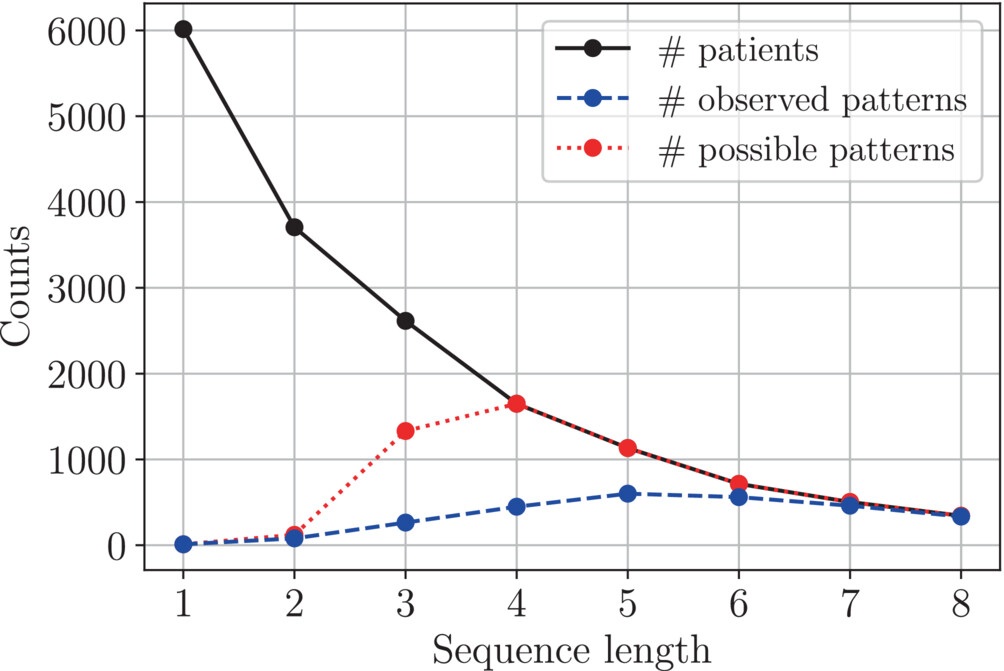

Fast Treatment Personalization with Latent Bandits in Fixed-Confidence Pure Exploration

May 3, 2023

Personalizing treatments for patients often involves a period of trial-and-error search until an optimal choice is found. To minimize suffering and other costs, it is critical to make this process as short as possible. When treatments have primarily short-term effects, search can be performed with multi-armed bandits (MAB), but these typically require long exploration periods to guarantee optimality. In this work, we design MAB algorithms which provably identify optimal treatments quickly by leveraging prior knowledge of the types of decision processes (patients) we can encounter, in the form of a latent variable model. We present two algorithms, the Latent LP-based Track and Stop (LLPT) explorer and the Divergence Explorer for this setting: fixed-confidence pure-exploration latent bandits. We give a lower bound on the stopping time of any algorithm which is correct at a given certainty level, and prove that the expected stopping time of the LLPT Explorer matches the lower bound in the high-certainty limit. Finally, we present results from an experimental study based on realistic simulation data for Alzheimer's disease, demonstrating that our formulation and algorithms lead to a significantly reduced stopping time.

Time series of satellite imagery improve deep learning estimates of neighborhood-level poverty in Africa

Apr 25, 2023

To combat poor health and living conditions, policymakers in Africa require temporally and geographically granular data measuring economic well-being. Machine learning (ML) offers a promising alternative to expensive and time-consuming survey measurements by training models to predict economic conditions from freely available satellite imagery. However, previous efforts have failed to utilize the temporal information available in earth observation (EO) data, which may capture developments important to standards of living. In this work, we develop an EO-ML method for inferring neighborhood-level material-asset wealth using multi-temporal imagery and recurrent convolutional neural networks. Our model outperforms state-of-the-art models in several aspects of generalization, explaining 72% of the variance in wealth across held-out countries and 75% held-out time spans. Using our geographically and temporally aware models, we created spatio-temporal material-asset data maps covering the entire continent of Africa from 1990 to 2019, making our data product the largest dataset of its kind. We showcase these results by analyzing which neighborhoods are likely to escape poverty by the year 2030, which is the deadline for when the Sustainable Development Goals (SDG) are evaluated.

Sharing pattern submodels for prediction with missing values

Oct 20, 2022

Missing values are unavoidable in many applications of machine learning and present a challenge both during training and at test time. When variables are missing in recurring patterns, fitting separate pattern submodels have been proposed as a solution. However, independent models do not make efficient use of all available data. Conversely, fitting a shared model to the full data set typically relies on imputation which may be suboptimal when missingness depends on unobserved factors. We propose an alternative approach, called sharing pattern submodels, which make predictions that are a) robust to missing values at test time, b) maintains or improves the predictive power of pattern submodels, and c) has a short description enabling improved interpretability. We identify cases where sharing is provably optimal, even when missingness itself is predictive and when the prediction target depends on unobserved variables. Classification and regression experiments on synthetic data and two healthcare data sets demonstrate that our models achieve a favorable trade-off between pattern specialization and information sharing.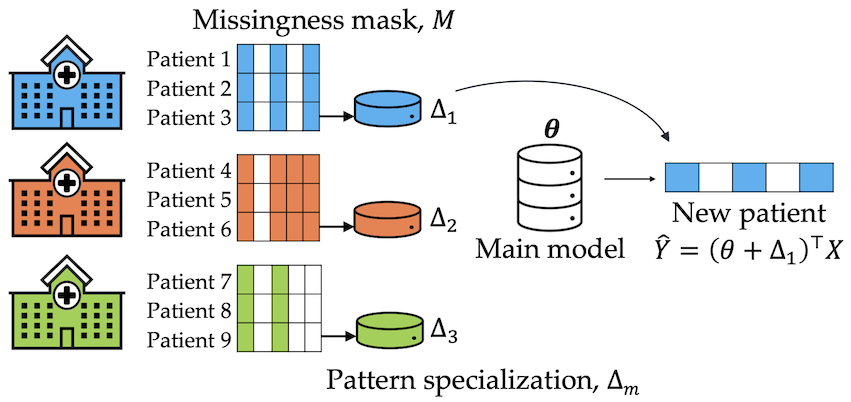

NeurIPS 2022: Efficient learning of nonlinear prediction models with time-series privileged information

Sep 15, 2022

In domains where sample sizes are limited, efficient learning algorithms are critical. Learning using privileged information (LuPI) offers increased sample efficiency by allowing prediction models access to types of information at training time which is unavailable when the models are used. In recent work, it was shown that for prediction in linear-Gaussian dynamical systems, a LuPI learner with access to intermediate time series data is never worse and often better in expectation than any unbiased classical learner. We provide new insights into this analysis and generalize it to nonlinear prediction tasks in latent dynamical systems, extending theoretical guarantees to the case where the map connecting latent variables and observations is known up to a linear transform. In addition, we propose algorithms based on random features and representation learning for the case when this map is unknown. A suite of empirical results confirm theoretical findings and show the potential of using privileged time-series information in nonlinear prediction.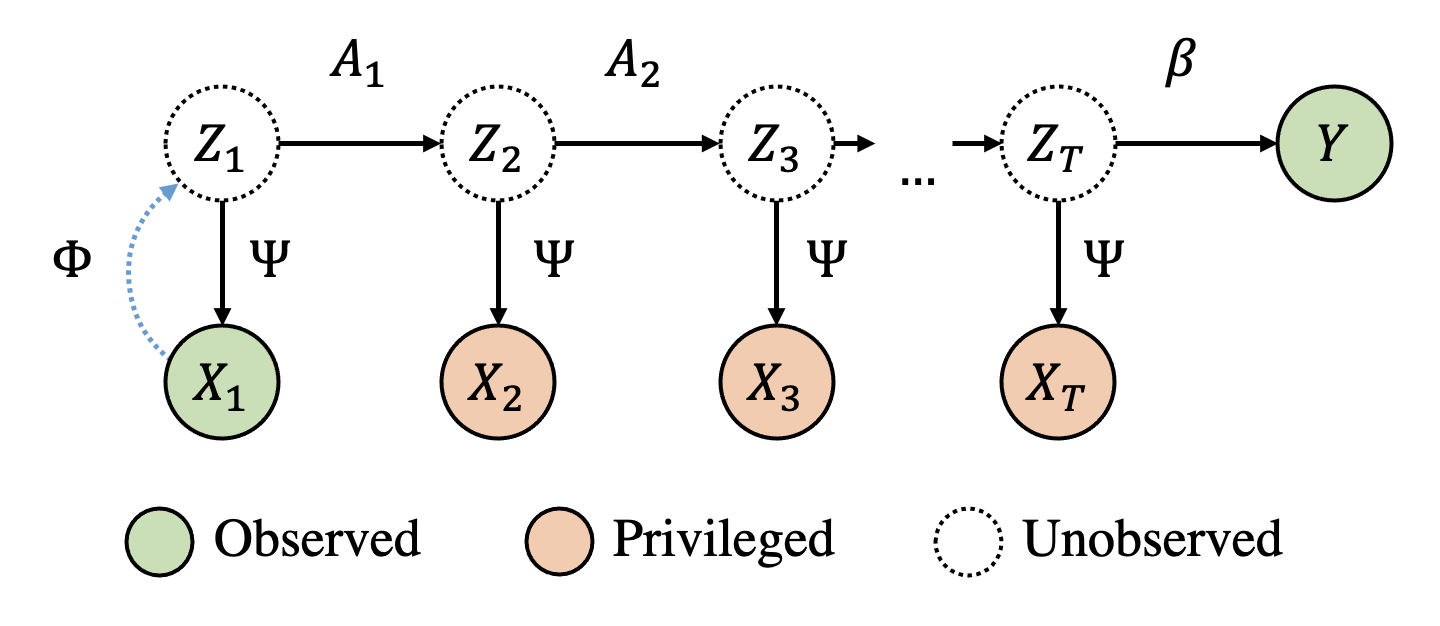

Seminar: Efficient learning of nonlinear prediction models with time-series privileged information

Sep 12, 2022

In domains where sample sizes are limited, efficient learning is critical. Yet, there are machine learning problems where standard practice routinely leaves substantial information unused. One example is prediction of an outcome at the end of a time series based on variables collected at a baseline time point, for example, the 30-day risk of mortality for a patient upon admission to a hospital. In applications, it is common that intermediate samples, collected between baseline and end points, are discarded, as they are not available as input for prediction when the learned model is used. We say that this information is privileged, as it is available only at training time. In this talk, we show that making use of privileged information from intermediate time series can lead to much more efficient learning. We give conditions under which it is provably preferable to classical learning, and a suite of empirical results to support these findings.

Practicality of generalization guarantees for unsupervised domain adaptation with neural networks

Sep 2, 2022

Understanding generalization is crucial to confidently engineer and deploy machine learning models, especially when deployment implies a shift in the data domain. For such domain adaptation problems, we seek generalization bounds which are tractably computable and tight. If these desiderata can be reached, the bounds can serve as guarantees for adequate performance in deployment. However, in applications where deep neural networks are the models of choice, deriving results which fulfill these remains an unresolved challenge; most existing bounds are either vacuous or has non-estimable terms, even in favorable conditions. In this work, we evaluate existing bounds from the literature with potential to satisfy our desiderata on domain adaptation image classification tasks, where deep neural networks are preferred. We find that all bounds are vacuous and that sample generalization terms account for much of the observed looseness, especially when these terms interact with measures of domain shift. To overcome this and arrive at the tightest possible results, we combine each bound with recent data-dependent PAC-Bayes analysis, greatly improving the guarantees. We find that, when domain overlap can be assumed, a simple importance weighting extension of previous work provides the tightest estimable bound. Finally, we study which terms dominate the bounds and identify possible directions for further improvement.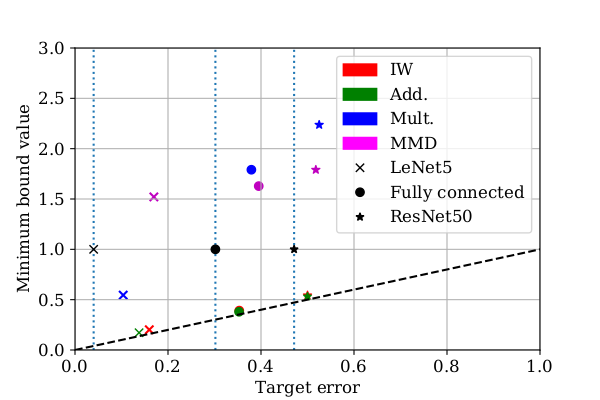

Case-Based Off-Policy Evaluation Using Prototype Learning

Jul 27, 2022

Importance sampling (IS) is often used to perform off-policy evaluation but it is prone to several issues---especially when the behavior policy is unknown and must be estimated from data. Significant differences between target and behavior policies can result in uncertain value estimates due to, for example, high variance. Standard practices such as inspecting IS weights may be insufficient to diagnose such problems and determine for which type of inputs the policies differ in suggested actions and resulting values. To address this, we propose estimating the behavior policy for IS using prototype learning. The learned prototypes provide a condensed summary of the input-action space, which allows for describing differences between policies and assessing the support for evaluating a certain target policy. In addition, we can describe a value estimate in terms of prototypes to understand which parts of the target policy have the most impact on the estimate. We find that this provides new insights in the examination of a learned policy for sepsis management. Moreover, we study the bias resulting from restricting models to use prototypes, how bias propagates to IS weights and estimated values and how this varies with history length.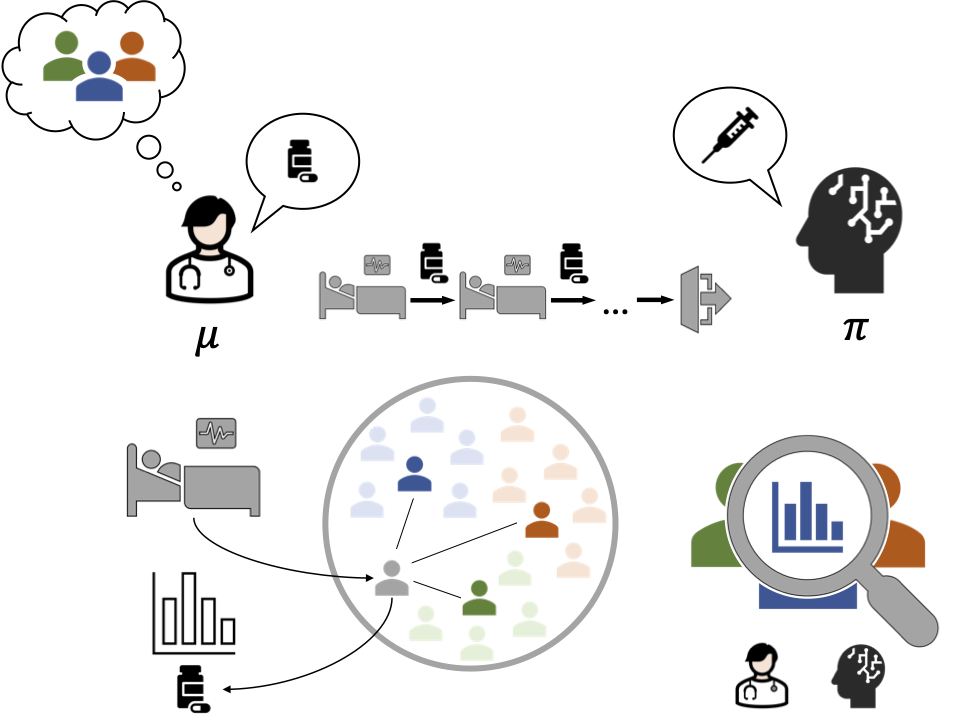

ADCB: An Alzheimer’s disease simulator for benchmarking observational estimators of causal effects

Apr 7, 2022

Simulators make unique benchmarks for causal effect estimation as they do not rely on unverifiable assumptions or the ability to intervene on real-world systems. This is especially important for estimators targeting healthcare applications as possibilities for experimentation are limited with good reason. We develop a simulator of clinical variables associated with Alzheimer’s disease, aimed to serve as a benchmark for causal effect estimation while modeling intricacies of healthcare data. We fit the system to the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset and ground hand-crafted components in results from comparative treatment trials and observational treatment patterns. The simulator includes parameters which alter the nature and difficulty of the causal inference tasks, such as latent variables, effect heterogeneity, length of observed subject history, behavior policy and sample size. We use the simulator to compare standard estimators of average and conditional treatment effects.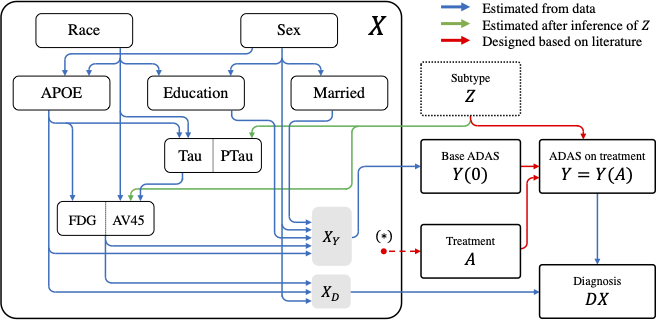

Learning using privileged time series information

Feb 1, 2022

We study prediction of future outcomes with supervised models that use privileged information during learning. The privileged information comprises samples of time series observed between the baseline time of prediction and the future outcome; this information is only available at training time which differs from the traditional supervised learning. Our question is when using this privileged data leads to more sample-efficient learning of models that use only baseline data for predictions at test time. We give an algorithm for this setting and prove that when the time series are drawn from a non-stationary Gaussian-linear dynamical system of fixed horizon, learning with privileged information is more efficient than learning without it. On synthetic data, we test the limits of our algorithm and theory, both when our assumptions hold and when they are violated. On three diverse real-world datasets, we show that our approach is generally preferable to classical learning, particularly when data is scarce. Finally, we relate our estimator to a distillation approach both theoretically and empirically.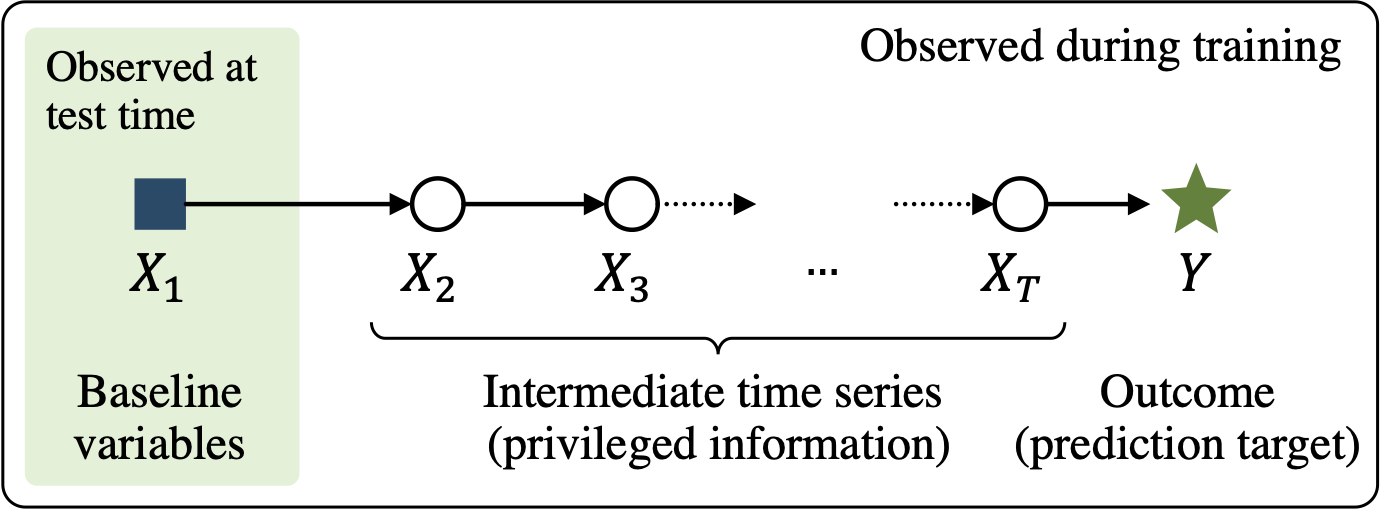

Predicting progression & cognitive decline in amyloid-positive patients with Alzheimer's disease

Mar 15, 2021

In Alzheimer’s disease, amyloid-β (Aβ) peptides aggregate in the brain forming CSF amyloid levels, which are a key pathological hallmark of the disease. However, CSF amyloid levels may also be present in cognitively unimpaired elderly individuals. Therefore, it is of great value to explain the variance in disease progression among patients with Aβ pathology. We studied the problem of predicting disease progression and cognitive decline of potential AD patients with established Aβ pathology using the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database.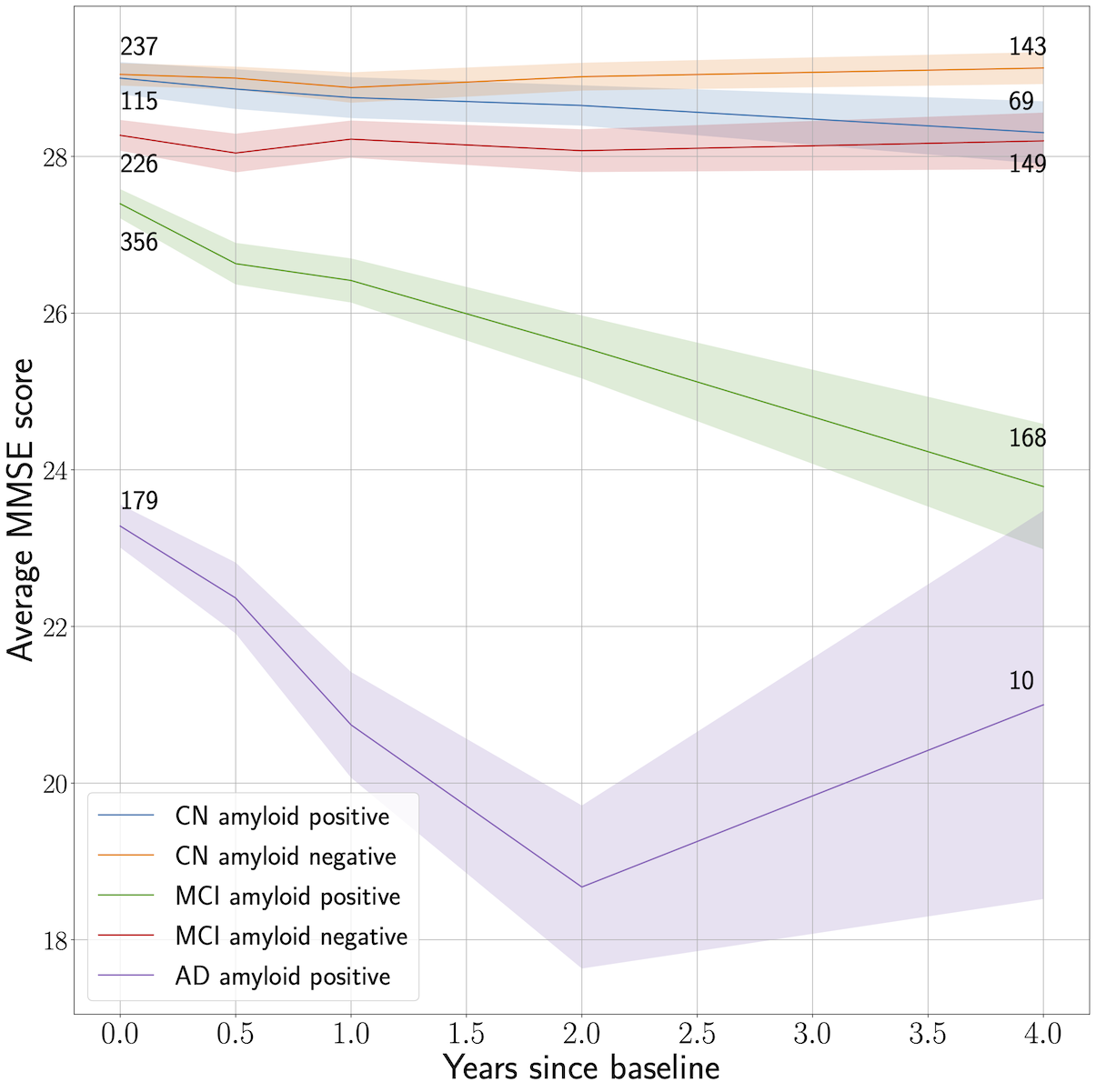

Tocilizumab treatment for rheumatoid arthritis

Feb 1, 2021

As of September 2020, the division of Data Science & AI have four brand new PhD students with Fredrik Johansson as main advisor. This marks the start of the Healthy AI lab at Chalmers University of Technology. Adam Breitholtz, Newton Mwai, Lena Stempfle and Anton Matsson begin their doctoral studies, funded by the Wallenberg AI, Autonomous Systems and Software programme.

Learning to search efficiently for causally near-optimal treatments

Dec 31, 2020

Finding an effective medical treatment often requires a search by trial and error. Making this search more efficient by minimizing the number of unnecessary trials could lower both costs and patient suffering. We formalize this problem as learning a policy for finding a near-optimal treatment in a minimum number of trials using a causal inference framework. We give a model-based dynamic programming algorithm which learns from observational data while being robust to unmeasured confounding. To reduce time complexity, we suggest a greedy algorithm which bounds the near-optimality constraint. The methods are evaluated on synthetic and real-world healthcare data and compared to model-free reinforcement learning. We find that our methods compare favorably to the model-free baseline while offering a more transparent trade-off between search time and treatment efficacy.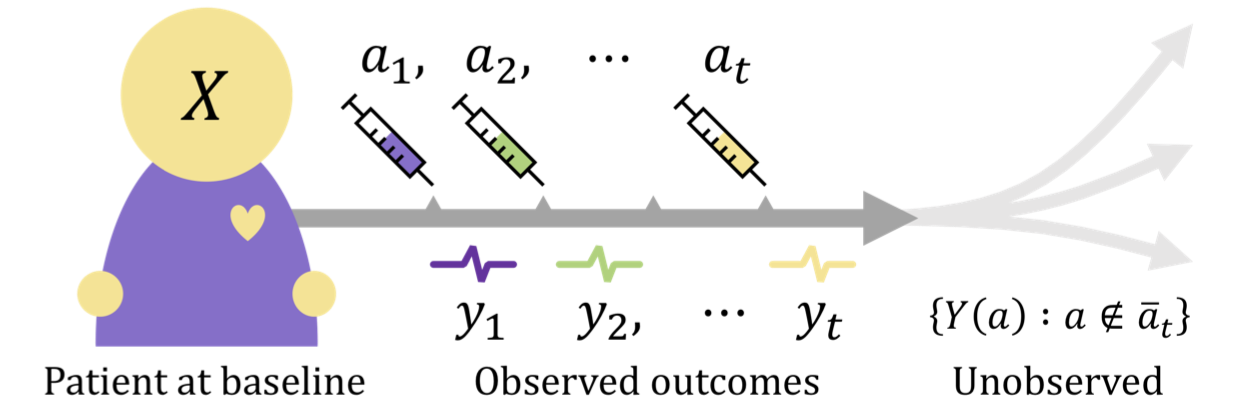

A new group: The Healthy AI lab!

Sep 1, 2020

As of September 2020, the division of Data Science & AI have four brand new PhD students with Fredrik Johansson as main advisor. This marks the start of the Healthy AI lab at Chalmers University of Technology. Adam Breitholtz, Newton Mwai, Lena Stempfle and Anton Matsson begin their doctoral studies, funded by the Wallenberg AI, Autonomous Systems and Software programme.